La teoría moderna de los portafolios es una teoría desarrollada por Harry Markowitz. Consiste en construir una cartera de inversión que maximice los retornos para cada nivel de riesgo al abordar la cartera como un todo, analizando la correlación de los retornos entre los diferentes activos.
Entendiendo la MPT
La teoría moderna de los portafolios sostiene que las características de riesgo y rendimiento de una inversión no deben considerarse de manera individual, sino que deben evaluarse según la forma en que el activo afecta al riesgo y al rendimiento general de la cartera.
La MPT muestra cómo el inversor puede construir una cartera de múltiples activos, bien diversificada, que maximice sus beneficios para el nivel de riesgo e incertidumbre que esté dispuesto a asumir, según medidas estadísticas como la varianza y la correlación.
El rendimiento esperado de la cartera se calcula como una suma ponderada de los retornos de los activos individuales. Si una cartera contuviera cuatro activos igualmente ponderados con rendimientos esperados de 4, 6, 10 y 14%, el rendimiento esperado de la cartera sería:
(4% x 25%) + (6% x 25%) + (10% x 25%) + (14% x 25%) = 8.5%
El riesgo de la cartera es una función de las variaciones de los retornos de cada activo y de sus correlaciones entre sí.
Para calcular el riesgo de una cartera de cuatro activos, el inversor necesita cada una de las variaciones de los cuatro activos y sus seis correlaciones, ya que hay seis posibles combinaciones de dos activos con cuatro activos.
Debido a las correlaciones de activos, el riesgo total de la cartera, o desviación estándar, es menor que lo que se calcularía mediante una suma ponderada.
Diversificación
La diversificación es una estrategia de asignación de cartera que tiene como objetivo minimizar el riesgo idiosincrásico mediante la tenencia de activos que no están perfectamente correlacionados. Para entender mejor podemos usar la analogía de no poner todos los huevos en la misma canasta.
Una correlación positiva perfecta entre los activos dentro de una cartera aumenta la desviación estándar / riesgo de la cartera. La diversificación reduce el riesgo idiosincrásico al mantener una cartera de activos que no están perfectamente correlacionados de manera positiva.
Por ejemplo, suponga que una cartera consta de los activos A y B. El coeficiente de correlación para A y B es -0,9. La figura muestra una fuerte correlación negativa: por lo que es probable que una pérdida en A sea compensada por una ganancia en B.
Sin embargo la diversificación tiene sus límites, el riesgo sistemático o de mercado no puede ser diversificado, a medida que los mercados se interrelacionan se vuelve aún más difícil reducir este riesgo.
Frontera eficiente
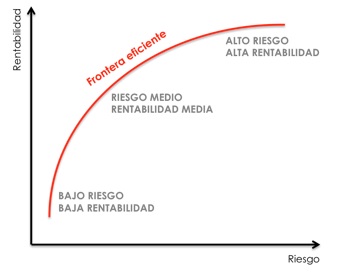
Cada posible combinación de activos puede ser dibujada en un gráfico representando el riesgo en un eje y el retorno esperado en el otro eje.
Este gráfico muestra las carteras más eficientes. Por ejemplo una cartera con un retorno esperado de 7% y una desviación estándar de 12% se considera más eficiente que otra cartera con un retorno esperado de 7% y una desviación estándar de 15%.
Si dibujamos una línea que atraviese todas las carteras más eficientes obtenemos lo que se llama la frontera eficiente. Según la teoría, no es interesante invertir en cualquier activo que no esté en esta línea.
Paso a paso
- Hallar el valor esperado de los diferentes activos
- Hallar la volatilidad de los retornos de cada activo
- Hallar la matriz de correlación
- Definir el coeficiente de aversión al riesgo
- Hallar los pesos para cada activo.
Críticas a MPT
Si bien la teoría moderna de los portafolios tiene muchos beneficios, también tiene sus contras, principalmente por tener varios supuestos poco realistas.
- Requiere redefinir el concepto de riesgo, de pérdida a incertidumbre.
- Asume que es posible seleccionar instrumentos cuyos rendimientos sean independientes; sin embargo, está demostrado que, en periodos de crisis, estos actúan de manera correlacionada.
- Muchas veces requiere de técnicas sofisticadas, como ir en corto, o de instrumentos complejos, como los futuros y las opciones.
- Pesa a las ganancias y a las pérdidas de manera simétrica.
Glosario Estadístico
Riesgo/Desviación Típica Definimos al riesgo como la desviación estándar de los retornos esperados
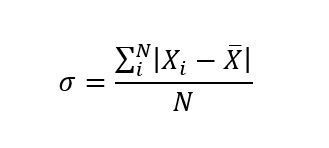
X: Promedio
N: número de observaciones
Valor esperado
Es un valor promedio a largo plazo de variables aleatorias. También indica el promedio ponderado por probabilidad de todos los valores posibles.
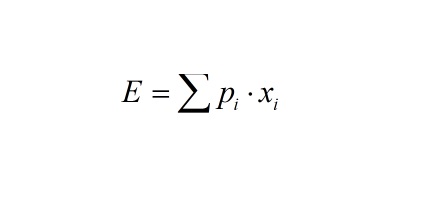
P: probabilidad de que ocurra
X: Valor del suceso
Covarianza
Es una medida que nos dice la dirección en la que dos variables se mueven. Por ejemplo, el número de paraguas vendidos y la cantidad de días de lluvia tendrán una covarianza positiva, y el número de crímenes por habitante y la cantidad de patrullas por las calles tendrían una covarianza negativa.
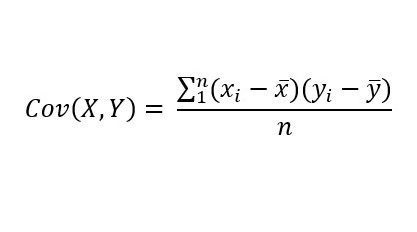
Yi: observación de Y
X: promedio de X
Y: promedio de Y
N: número de observaciones.
Correlación
Es una medida similar a la covarianza pero además de la dirección, también nos indica la fuerza con la que se mueven en conjunto. Su valor va desde -1 (correlación negativa) hasta 1 (correlación perfecta), 0 vendría a ser la ausencia total de correlación.
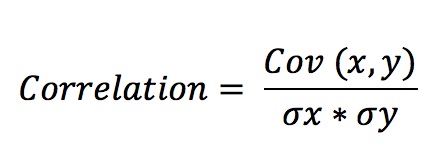
Ox: desviación típica de x
Oy: desviación típica de y





