El Dilema del Prisionero es una rama de la Teoría de Juegos que explica el problema en la toma de decisiones en un ambiente competitivo, esto en la economía se observa en los mercados de oligopolio que, por sus características, poseen pocos participantes y las decisiones de optimización de sus beneficios dependen de la decisión de los competidores.
Esta teoría se plantea el escenario en el que dos prisioneros (los cuales representan a los participantes del mercado y sus decisiones que representan los beneficios que se obtendrán) son interrogados sin pruebas suficientes sobre sus crímenes y dado que un prisionero no sabe la respuesta del otro prisionero.
Dependiendo de lo que uno diga, esto podría afectar al otro de las siguientes maneras:
- Si el prisionero A delata al prisionero B, el prisionero B tendrá 10 años de prisión y el A 2 años
- Si el prisionero B delata al prisionero A, el prisionero A tendrá 10 años de prisión y el B 2 años
- Si los 2 se delatan, tendrán 5 años de prisión.
- Si los 2 se quedan callados, los 2 tendrán 1 año de prisión.
En la siguiente tabla se representan los distintos escenarios, en base a las posibles decisiones de los jugadores y los respectivos beneficios que obtendrán:
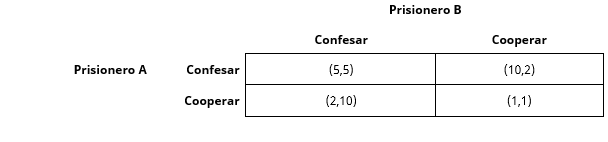
A la hora de analizar las estrategias se concluye que:
- Si uno de los 2 decide delatar al otro, esto provocará que el que no confiesa tenga 10 años de prisión, pero, el que delate solo 2 por lo tanto, esta estrategia solo es conveniente para 1 parte (Equilibrio de Nash).
- Si los 2 confiesan tendrán 5 años de prisión cada uno; sin embargo, si los 2 cooperasen, sin embargo, aunque esta sea la mejor opción al no saber qué hará el otro prisionero, lo más probable es que ambos se delaten (Óptimo de Pareto).
Conceptos complementarios:
- Equilibrio de Nash: situación en donde los individuos o jugadores no tienen ningún incentivo a cambiar su estrategia tomando en cuenta las decisiones de sus oponentes;
- Óptimo de Pareto: define toda situación en la que no es posible beneficiar a una persona sin perjudicar a otra.






