El ratio Sharpe fue desarrollado por William Sharpe, y permite a los inversionistas comparar los retornos de una inversión con el nivel de riesgo asumido.
Este ratio nos permite saber si los retornos de una inversión fueron consecuencia de decisiones inteligentes o de asumir más riesgo. A mayor ratio Sharpe mayor será el rendimiento ajustado al riesgo
Formula:
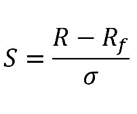
S: Ratio sharpe
R: Retorno
Rf: Tasa libre de riesgo
σ: Desviación standar
Restar la tasa libre de riesgo del rendimiento permite que un inversionista aísle mejor las ganancias asociadas con las actividades de toma de riesgos. La tasa de rendimiento libre de riesgo es el rendimiento de una inversión con cero riesgos, lo que significa que es el rendimiento que los inversores podrían esperar por no correr riesgos. El rendimiento de un bono del tesoro
El índice de Sharpe se puede utilizar para evaluar el rendimiento pasado de una cartera (ex-post) donde se utilizan los rendimientos reales en la fórmula. Alternativamente, un inversionista podría usar el rendimiento esperado de la cartera y la tasa libre de riesgo esperada para calcular un índice de Sharpe estimado (ex-ante).
El índice de Sharpe también puede ayudar a explicar si los rendimientos excesivos de una cartera se deben a decisiones de inversión inteligentes o son el resultado de un riesgo excesivo. Aunque una cartera o fondo puede disfrutar de rendimientos más altos que sus pares, solo es una buena inversión si esos rendimientos más altos no vienen con un exceso de riesgo adicional.
Cuanto mayor sea el índice de Sharpe de una cartera, mejor será su rendimiento ajustado al riesgo. Si el análisis da como resultado un índice de Sharpe negativo, significa que la tasa libre de riesgo es mayor que el rendimiento de la cartera o que se espera que el rendimiento de la cartera sea negativo. En cualquier caso, una relación de Sharpe negativa no transmite ningún significado útil.
Fuente: Sharpe Ratio Definition. (2022, 10 enero). Investopedia. https://www.investopedia.com/terms/s/sharperatio.asp






